平方根の計算
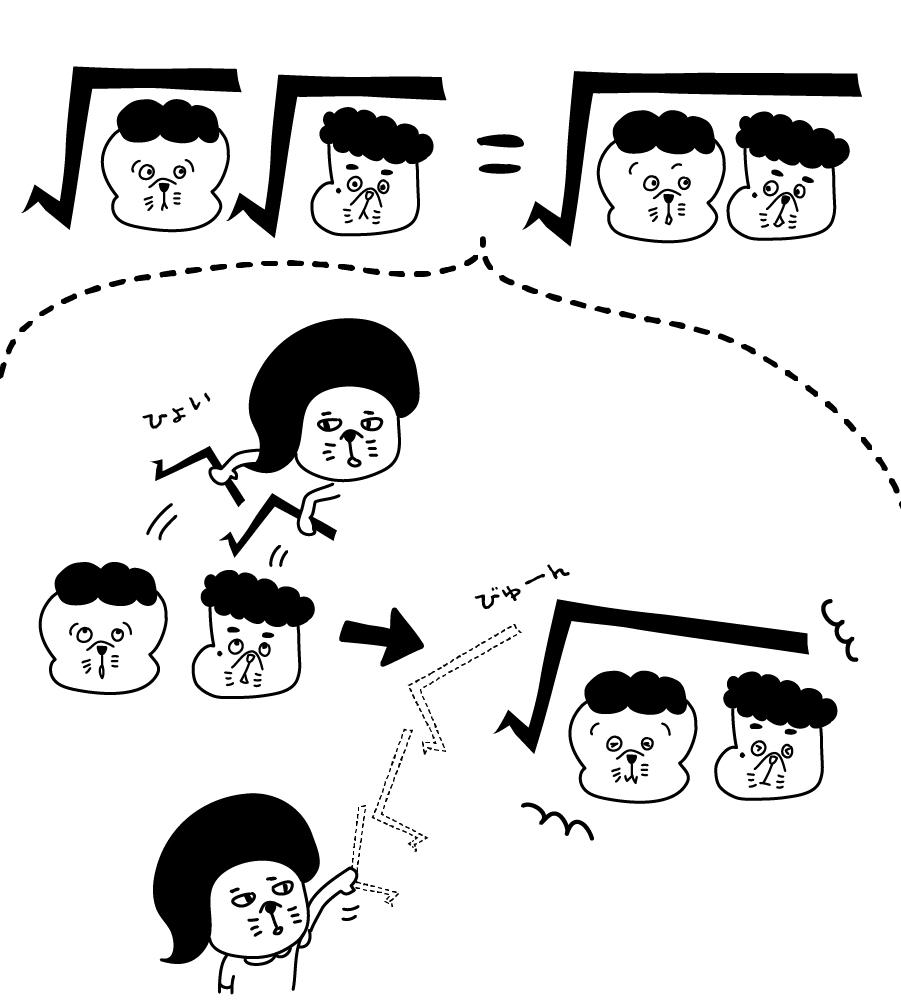
今までの計算と何か違う?
平方根の計算は今までの計算と違うのかな?
同じ数を2回掛けるといえば、正方形の面積だね。
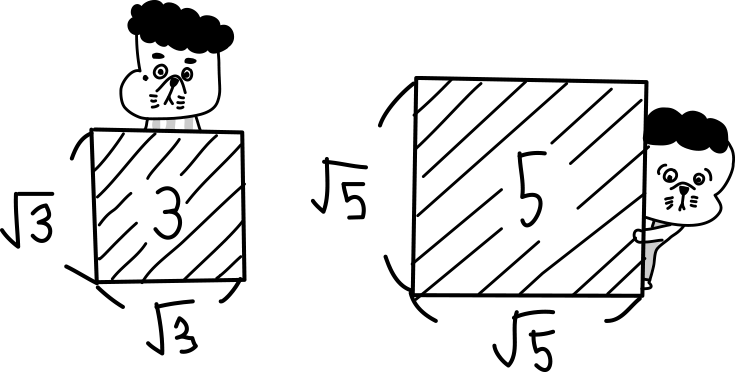
面積3の正方形と面積5の正方形の一辺の長さは根号を使って $\sqrt{3}$ と $\sqrt{5}$ って分かるね。
3 × 5 = 15 から面積15の正方形の一辺の長さは $\sqrt{15}$ ってことだよね。
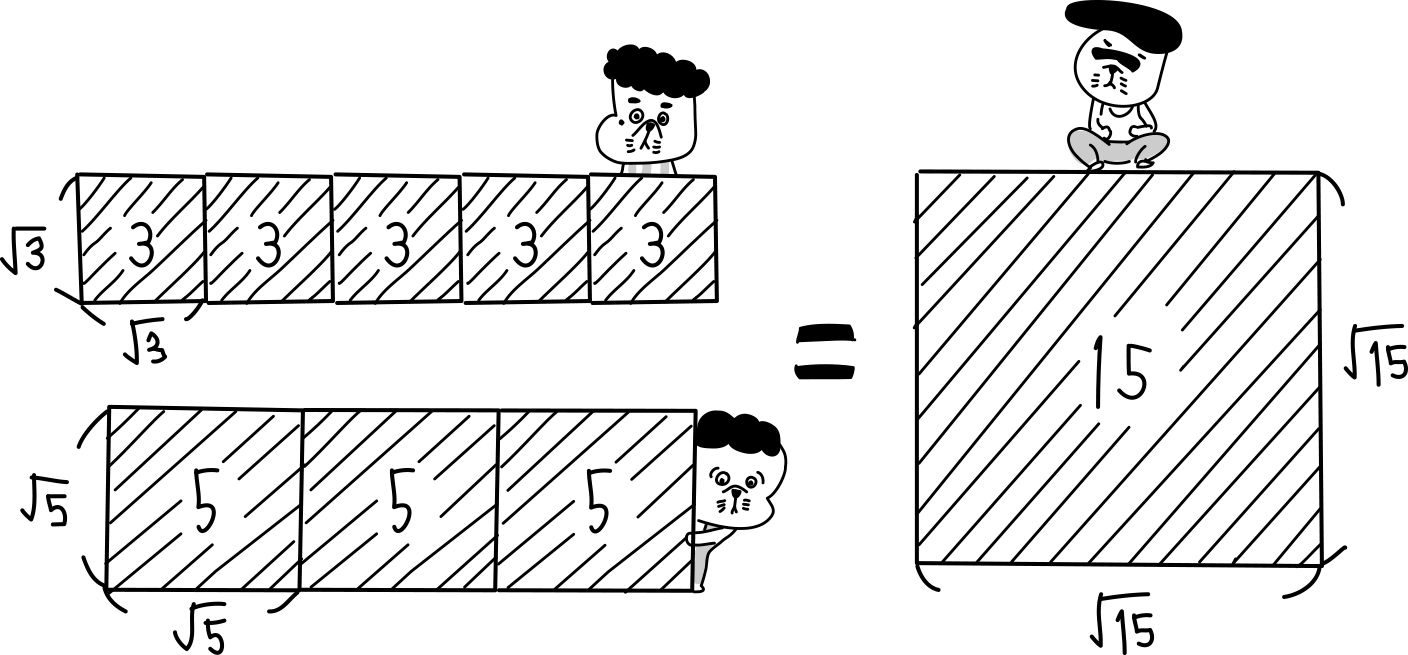
根号どうしのかけ算は根号を外して計算した値に根号を戻しても同じみたい。
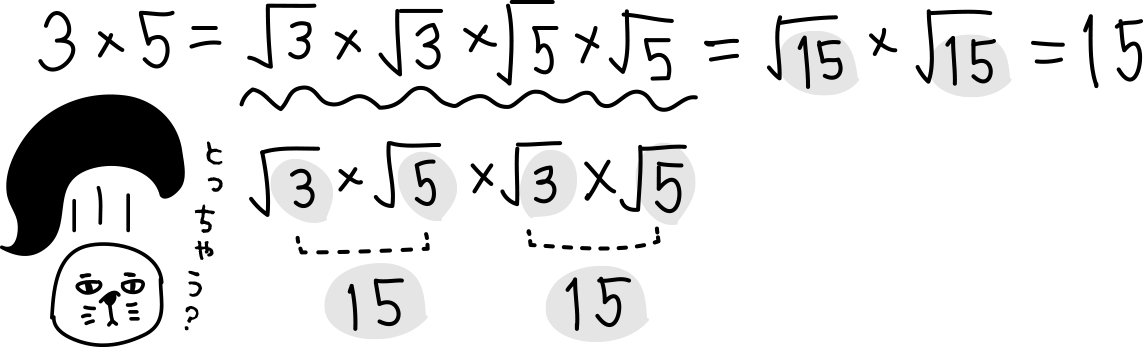
平方根の計算
平方根の計算をするときの性質をみていこう。
実数の範囲では四則が使え、交換法則・結合法則・分配法則が使えることを思い出して、実数 $x$ で積を考えてみよう。
$x = \sqrt{a}\sqrt{b} \ (a \gt 0 , b \gt 0)$ とおくと $x^{2}$ は
\begin{align}
x^{2} & = (\sqrt{a}\sqrt{b})^{2}\\
& = \sqrt{a}\sqrt{b}\sqrt{a}\sqrt{b}\\
& = \sqrt{a}\sqrt{a}\sqrt{b}\sqrt{b} \ \ \mbox{(交換法則)}\\
& = (\sqrt{a}\sqrt{a})(\sqrt{b}\sqrt{b}) \ \ \mbox{(結合法則)}\\
& = (\sqrt{a})^{2}(\sqrt{b})^{2}\\
& = ab
\end{align}
ここから
$$\sqrt{x^{2}} = \sqrt{ab}$$
がわかるね。
$x$ は最初に $a \gt 0 , b \gt 0$ としているから正の数なので
$x = \sqrt{ab}$ となって、$x$ を $\sqrt{a}\sqrt{b}$ に置き換えれば
$$\sqrt{a}\sqrt{b} = \sqrt{ab}$$
というのが分かるね。
同じように商も考える。
$x = \frac{\sqrt{a}}{\sqrt{b}} \ (a \gt 0 , b \gt 0)$ とおくと $x^{2}$ は
\begin{align}
x^{2} & = (\frac{\sqrt{a}}{\sqrt{b}})^{2}\\
& = \frac{\sqrt{a}}{\sqrt{b}}\frac{\sqrt{a}}{\sqrt{b}}\\
& = \frac{\sqrt{a}\sqrt{a}}{\sqrt{b}\sqrt{b}}\\
& = \frac{(\sqrt{a})^{2}}{(\sqrt{b})^{2}}\\
& = \frac{a}{b}
\end{align}
ここから
$$\sqrt{x^{2}} = \sqrt{\frac{a}{b}}$$
がわかるね。
$x$ は最初に $a \gt 0 , b \gt 0$ としているから正の数なので
$x = \sqrt{ab}$ となって、$x$ を $\frac{\sqrt{a}}{\sqrt{b}}$ に置き換えれば
$$\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$$
というのが分かるね。
さらに、$b$ を $m^{2}$ と考えると $\sqrt{a}\sqrt{b} = \sqrt{ab}$ , $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ より
$b = m^{2}$
$$m\sqrt{a} = \sqrt{m^{2}a} \ \ , \ \ \frac{\sqrt{a}}{m} = \sqrt{\frac{a}{m^{2}}}$$
この3つをまとめると
- 平方根の計算の性質
-
$a \gt 0 , b \gt 0$ のとき,
$$\sqrt{a}\sqrt{b} = \sqrt{ab} \ \ , \ \ \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$$
さらに $m \gt 0$ のとき,
$$\sqrt{m^{2}a} = m\sqrt{a}$$
だね。
