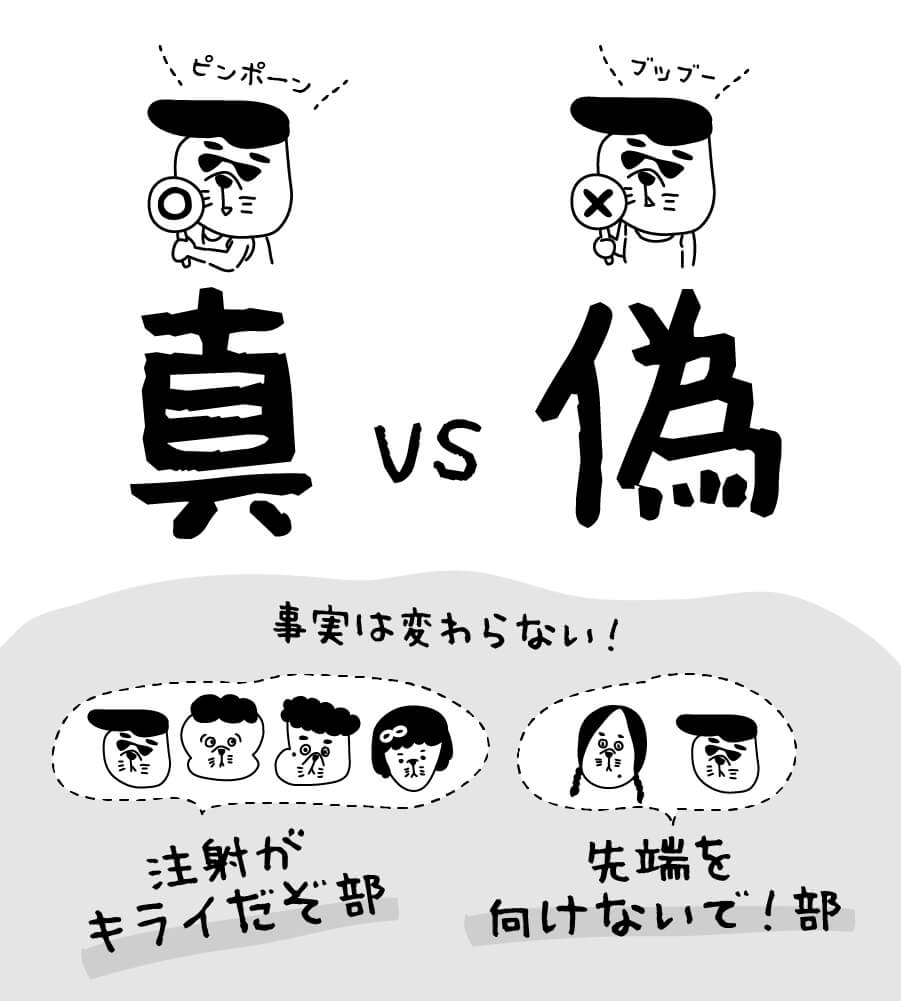
この2つの文章が正しいか正しくないかは、事実かどうか考えれば判断できるね。

数学にも、この式や文章は正しいのか、正しくないのか考えることがあるんだ。
そんな時、数学の表し方があるよ。

数学では、正しいか正しくないかが判断できる内容を式や文で表したものを命題というよ。

命題が正しいとき、その命題は真であるといい、
正しくないときは、その命題は偽であるというよ。

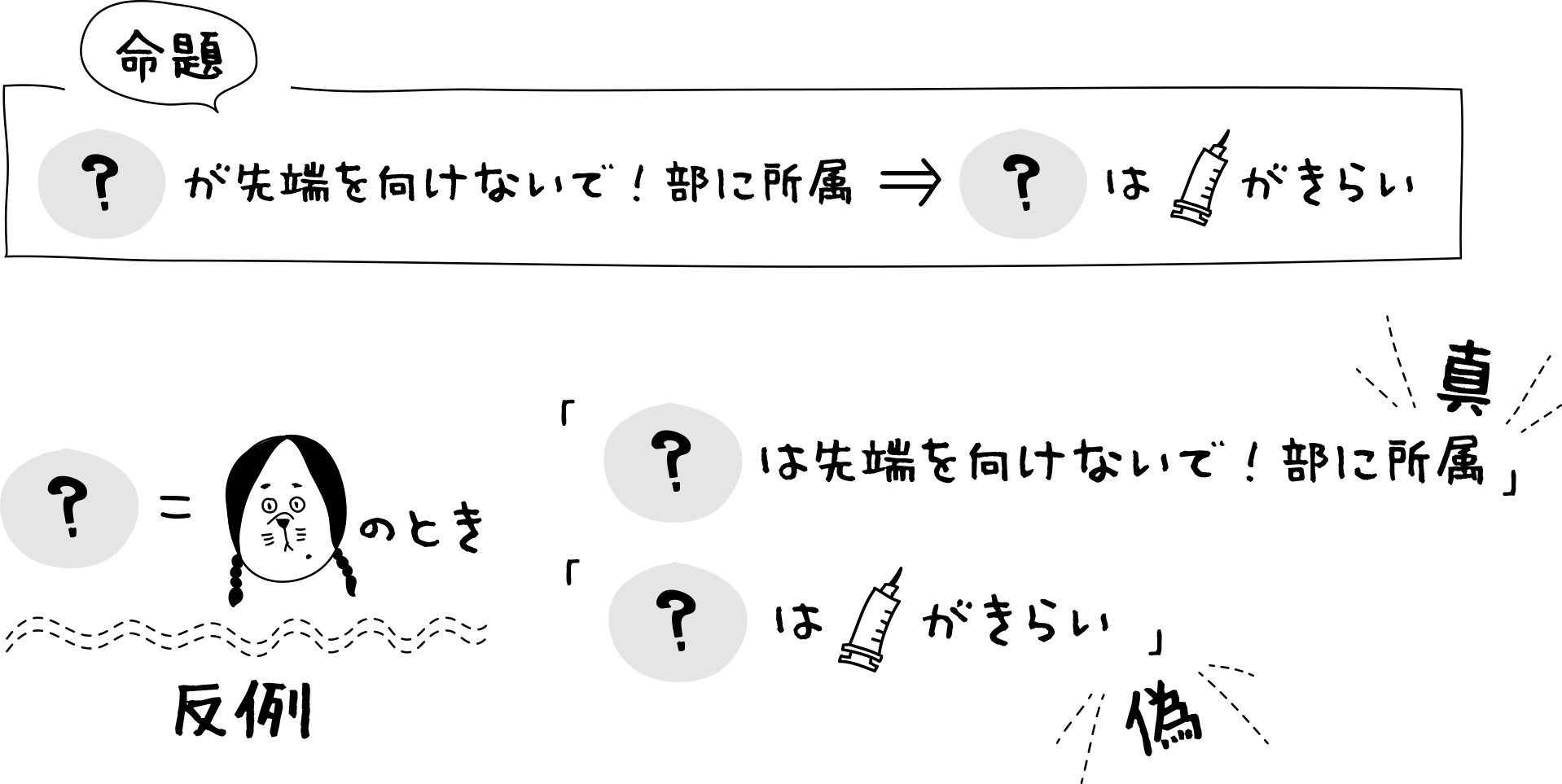
この(?)に、すーがはいれば正しいけど、
レイコが入ると正しくない・・・

レイコは注射はキライじゃないものね。
この文章が真になるには、「注射がキライ」が(?)の判断基準になるね。

数学だと(?)には色々な値が入る変数と考える。
そして、「注射がキライ」は変数に対して、正しいか正しくないかを判断する条件というよ。

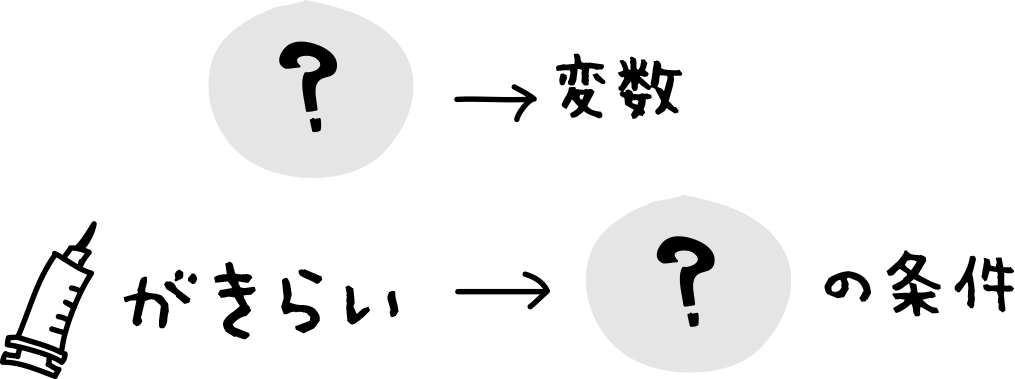
条件が真となるとき、その変数は条件を満たすというんだ。

命題は2つの条件p,qを”ならば”でつなげて、「pならばq」の形で表すことが多い。
この形の命題は、pは仮定、qは結論という。
記号を使って

と表す。

pは仮定だから”もし”を、qは常に正しい結論だから”いつだって”を命題の前につけると分かりやすいよ。

「p $\Rightarrow$ q」という命題が偽であることを示すには、仮定pから結論qに”いつだって”ならないことを示せばいいから、
仮定pのときqの条件を満たさない例を考えればいいね。
この例を反例というよ。