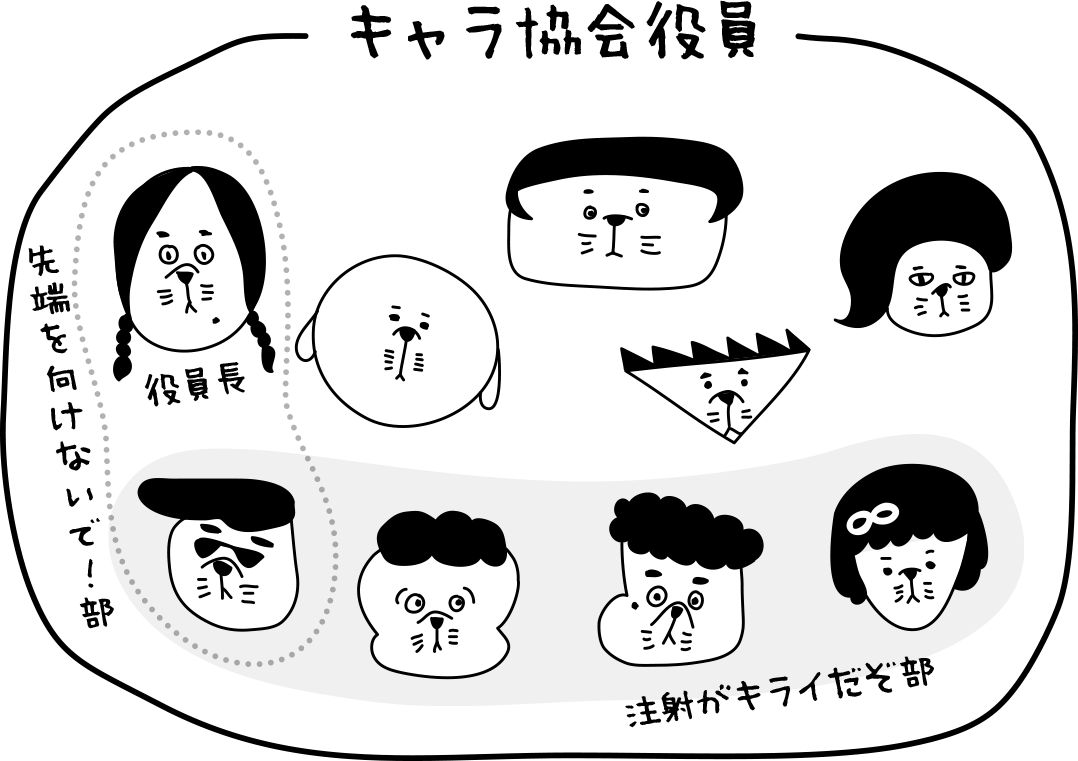
キャラ協会役員のメンバーは9人。注射がキライだぞ部のメンバーは4人。先端を向けないで!部のメンバーは2人。
じゃあ、注射がキライだぞ部と先端を向けないで!部のメンバーを合計すると何人?6人?

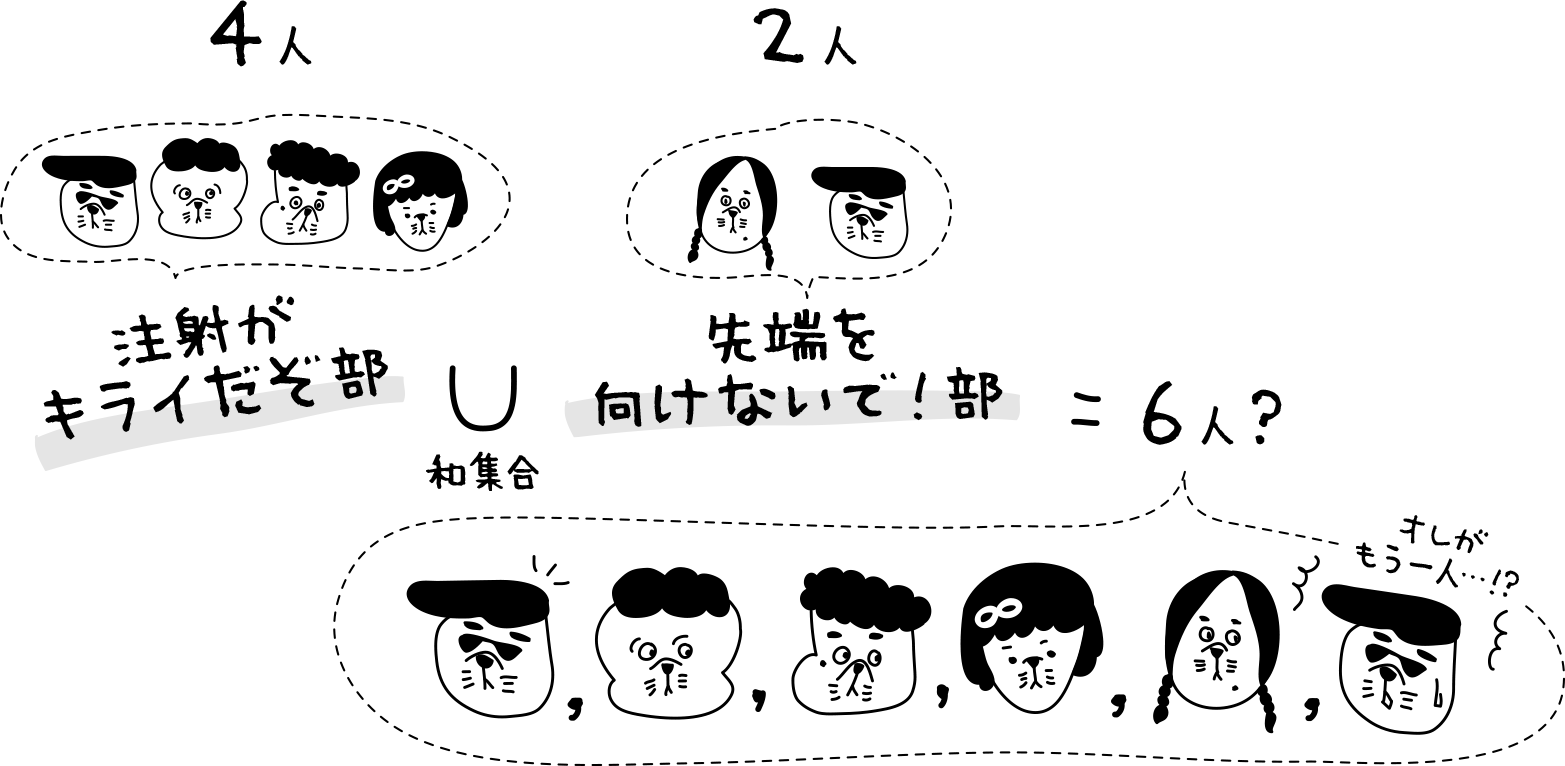
両方に所属しているヤンキーが2回登場しているよ。
でも、ヤンキーは双子じゃないから、ひとりしかいないはず。。。。
両方に所属しているヤンキーをダブって数えないようにしなきゃ！

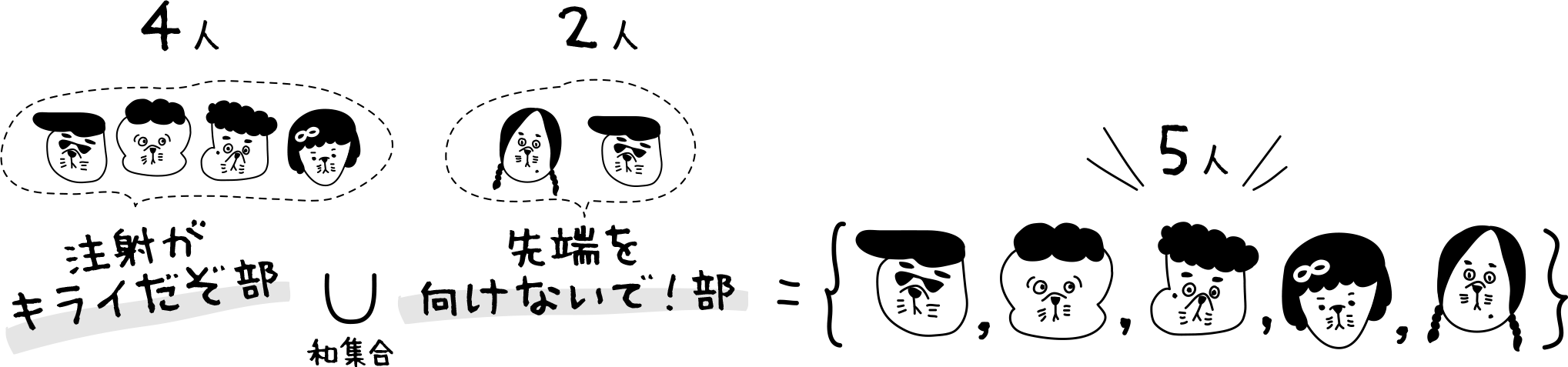
注射がキライだぞ部と先端を向けないで!部のメンバーの合計は5人だ。

有限集合A = {0,1,2}の要素は何個だろう？
すぐに要素が3個であると分かるね。

有限集合は要素の数が有限だから、個数をn(“集合名”)を使って表すよ。
集合Aの場合は要素が3個なので、n(A) = 3となる。

集合AとBが有限集合ならば、A $\cup$ Bも有限集合だね。では、A $\cup$ Bの要素の個数はどうなっているかな？
単純にn(A $\cup$ B) = n(A) + n(B)とすることはできるのかな？

例えば、集合A = {0,1,2}と集合B = {2,3,4}を考えてみよう。
n(A) = 3でn(B) = 3である。しかし、A $\cup$ B = {0,1,2,3,4}なので、n(A $\cup$ B) = 5である。
n(A $\cup$ B) = n(A) + n(B)とはならない。

集合AとBには共通する要素、A $\cap$ B = {2}があるからだね。

これをふまえると、下記のことがいえるよ。

空集合の要素の個数は0個だから、和集合の要素の個数は下記の式でまとめられるね。

和集合の要素の個数

n(A $\cup$ B) = n(A) + n(B) – n(A $\cap$ B)

全体集合Uが有限集合のとき、Uの部分集合AとAの補集合はどちらも有限集合だね。
集合AとAの補集合の和集合が全体集合Uになること、集合AとAの補集合の共通部分が空集合であることを思い出せば
各集合の要素の個数は下記のようになるね。

ここから補集合の要素の個数 n(A) を表す式は下記のようになって、
全体集合の要素の個数からAの要素の個数を引いた数だって分かるね。

補集合の要素の個数

n(A) = n(U) – n(A)

例えば、全体集合U = {0,1,2,3,4}とUの部分集合A = {0,1,2}を考えてみよう。
n(U) = 5でn(A) = 3だね。
Aの補集合Aの要素はA = {3,4}だからn(A) = 2だ。
n(A) = n(U) – n(A)が成立しているね。