今日は第5,555回目のキャラ協会役員の会議があった。
参加者は、レイコ、ると、ゴウ、サン、すー、ブンブン、しょうこ、ヤンキー、ぷくねーの9人だった。
よく見ると、“注射キライだぞ部”のメンバーが揃っているみたい。役員の中で“注射キライだぞ部”に所属していないのは誰だろう。

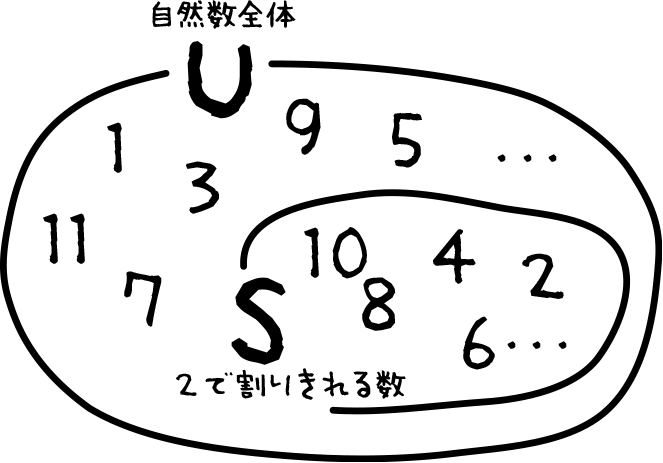自然数全体の集合を考えよう。
今はこの自然数全体の集合にめっちゃ注目して、要素全体の範囲にするぞ。
こんな時、範囲を決めて区切った集合全体を全体集合といって、Uで表すよ。

全体集合Uの中に、2で割り切れる自然数の集まりを集合Sとすると、集合Sは全体集合Uの部分集合だね。

この時、2で割り切れない自然数 = 集合Sに属さない要素たちを集合Sの補集合といって、集合名の上に横線を引いてSと表すよ。

キャラ協会の中で
注射がキライだぞ部と先端を向けないで!部の2つの部に所属していないのは、2つの部に所属しているヤンキー以外全員だ。
それは、注射がキライだぞ部に所属していないメンバーと先端を向けないで!部に所属していないメンバーを合わせたメンバーということになる。

逆に注射がキライだぞ部か先端を向けないで!部のどちらにも所属していないメンバーは、
注射がキライだぞ部に所属していないメンバーと先端を向けないで!部に所属していないメンバーのどちらにも該当するメンバーだ。

これを記号で表すと

となる。
キャラ協会を全体集合Uと考えて、注射がキライだぞ部を集合A、先端を向けないで!部を集合Bとすると

となるね。
この二つを合わせてド・モルガンの法則というよ。
この法則を覚えておくと、何かと便利なんだ。