実はレイコも先端恐怖症らしい。でも注射は怖くない。

ということで、先端恐怖症のレイコとヤンキーの2人は「先端を向けないで！部」をつくったみた。
ヤンキーは部を2つ掛け持ちすることになったよ。

2で割りきれる自然数の集合Sと3で割り切れる自然数の集合Tをみてみよう。

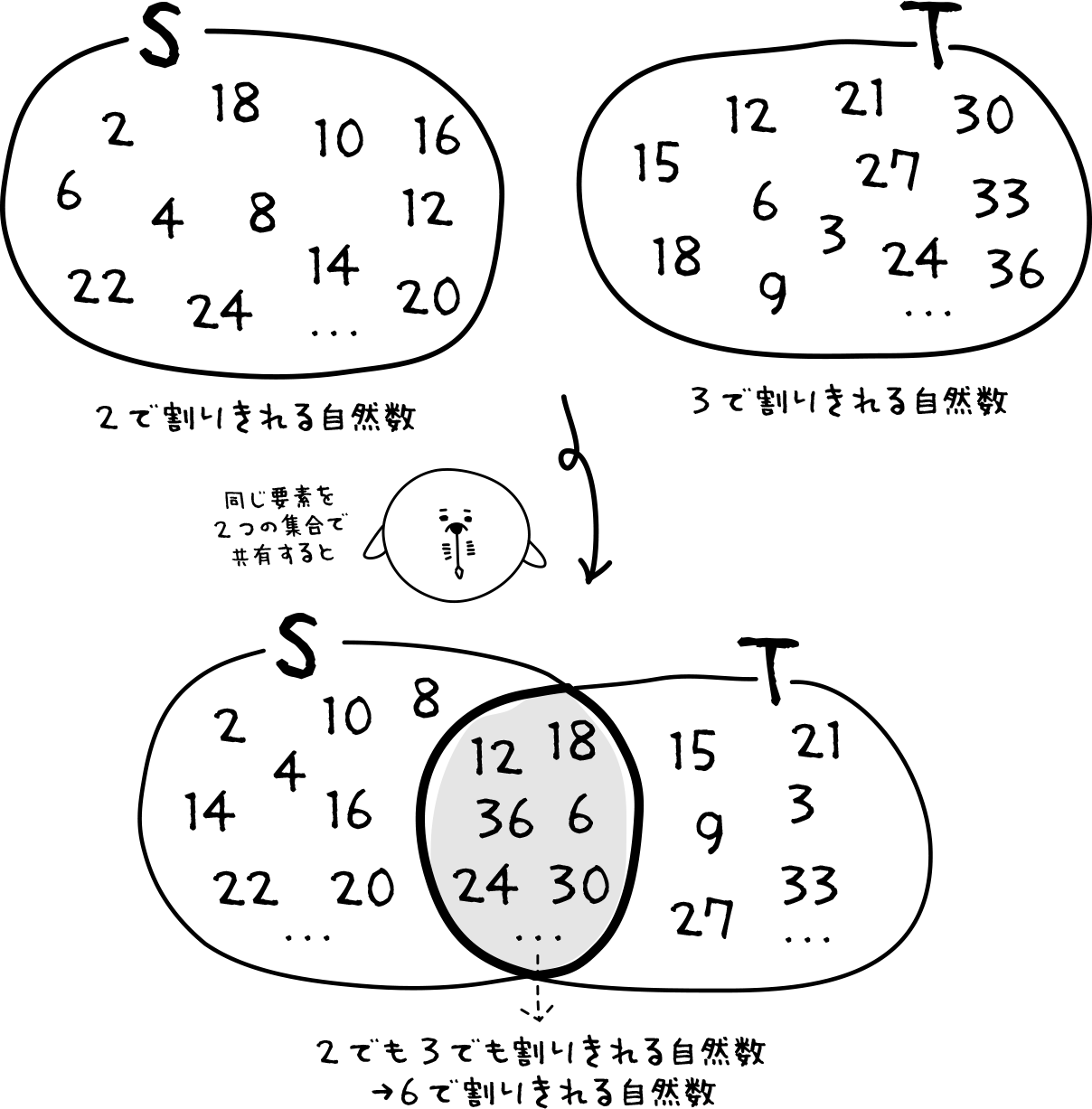
集合SとTは違う集合だけど、要素が同じものがある。この要素たちは2でも3でも割り切れる数、つまり6で割り切れる数だね。
この、集合SとTどちらにも属している要素たちを集めた集合を共有部分、または交わりといって、S $\cap$ Tで表す。

見方を変えてみよう。
どっちの集合にも属している要素ではなく、少なくてもどっちかの集合に属している要素を集めるとどうなる？
どっちかに属していればいいから、たとえば9は、9 $\notin$ S , 9 $\in$ TでOKだね。
4も、4 $\in$ S , 4 $\notin$ TでOKだね。

この、集合SとTに少なくてもどちらかに属している要素たちを集めた集合を和集合、または結びといって、S $\cup$ Tで表す。