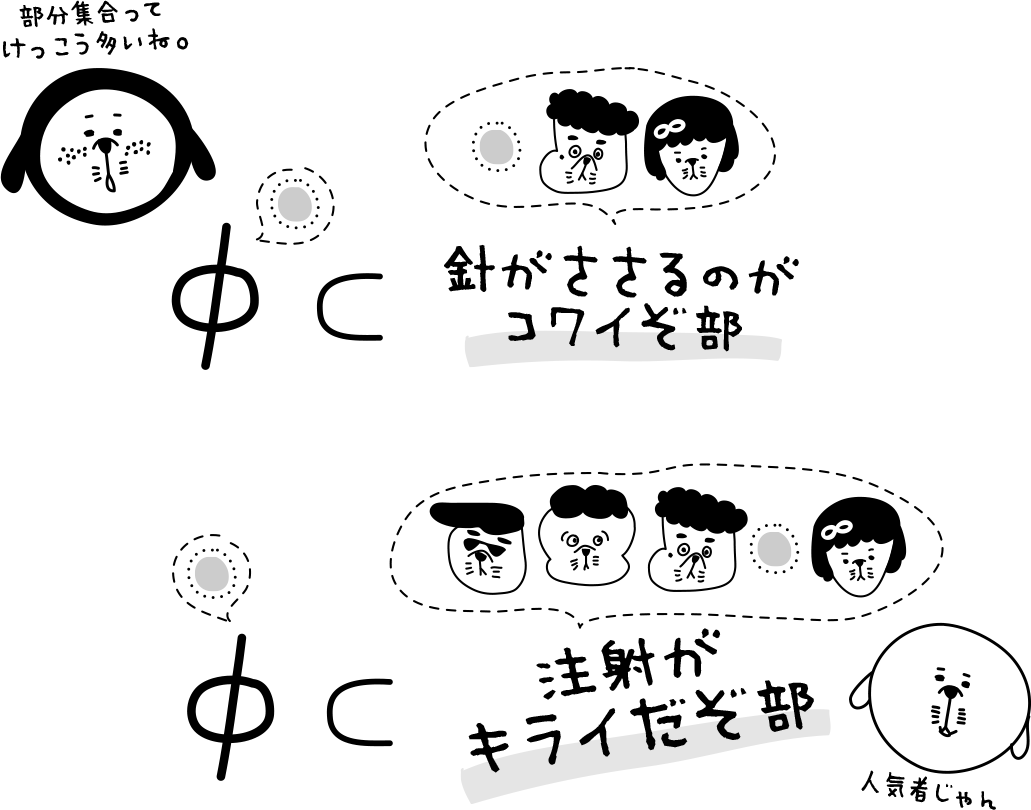
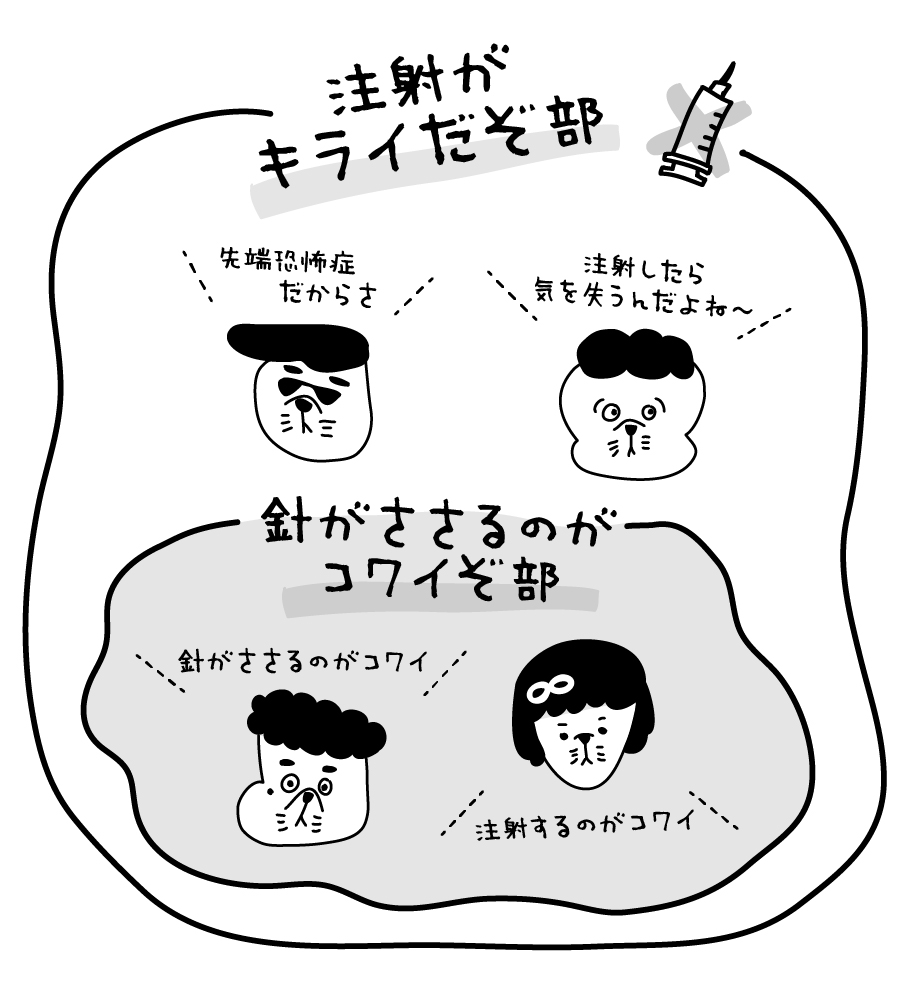
“注射キライだぞ部”のみんなに、なぜキライなのか聞いてみた。

しょうことすーは同じ理由だったので、この2人で“針が刺さるのがコワイぞ部”をつくることにした。

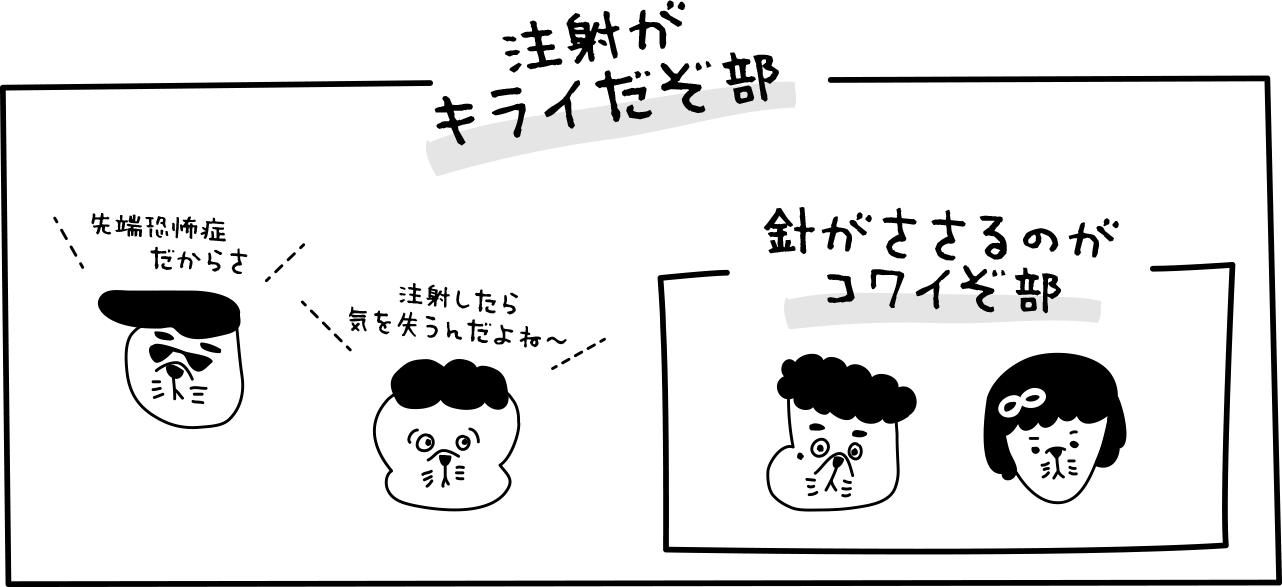
部内で新しい部ができちゃったよ。

集合P={1,2,3,4,5,6}と集合Q={2,4,6}を考えてみよう。

集合Pの中にすっぽり集合Qが入っている。
集合Qの要素が全て集合Pに属しているからだね。
この集合Qのことを集合Pの部分集合といって、Q$\subset$Pと表すよ。

今度は、要素が集合Pと全く同じ集合R={1,2,3,4,5,6}を考えてみよう。

これは…
R$\subset$Pであり、P$\subset$Rだね。
要素全体が同じ集合PとRは等しいといってP=Rで表すよ。

等しいといえば、集合Pはもちろん集合Pと等しいよね。だから集合P自身が集合Pの部分集合だといえるね。

記号$\subset$,$=$で表される集合同士の関係を包含ほうがん関係というんだ。

要素を1つももたない集合E={}を考えてみよう。
集合Eのような集合を空集合といって、記号Oで表すよ。

空集合はどの集合の中にも含まれているのが分かるかい？
どんな集合にも空集合は部分集合として存在するんだ。