分母の有理化
分母に根号がある!!!
分母に根号があると気にならない??気になるよね!?
$\frac{3}{0.1}$ とかもなんだかスッキリしないでしょ。それと同じFEELING!
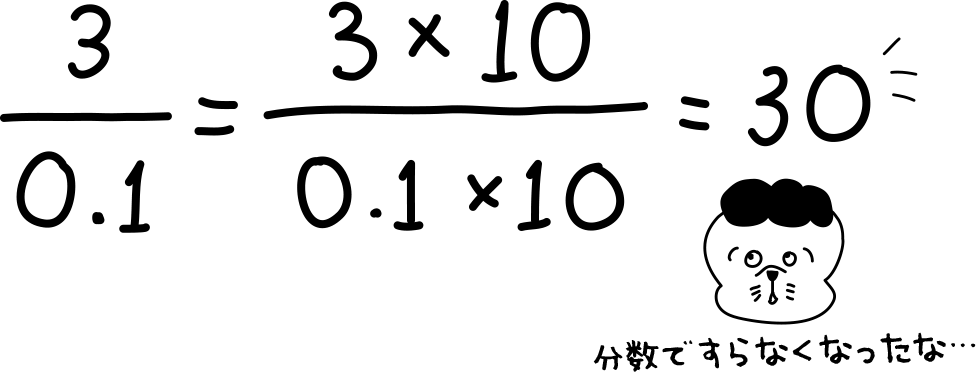
分母が違うもの同士の和や差の計算で分母を揃えるために分子と分母に同じ数を掛け合わせたね。
それを利用して分母の根号を消してみよう!
ふぅースッキリしたね。
分母の有理化
分母に根号が含む式を分母に根号のない式に直すことを分母の有理化というよ。
\begin{align}
\frac{2}{\sqrt{8}} & = \frac{2}{\sqrt{2}\sqrt{2}\sqrt{2}}\\
& = \frac{2}{2\sqrt{2}}\\
& = \frac{2\sqrt{2}}{2\sqrt{2}\sqrt{2}}\\
& = \frac{2\sqrt{2}}{2 \cdot 2}\\
& = \frac{\sqrt{2}}{2}
\end{align}
こんな風に変形させる。
分母に根号どうしの和や差がある場合は少し複雑になるよ。
こんなときは、乗法の公式を使うと便利!
- 乗法の公式
-
\begin{align}
x^{2} − y^{2} & = x^{2} + xy – xy − y^{2}\\
& = x(x+y)−y(x+y)\\
& = (x−y)(x+y)
\end{align}
を使って
\begin{align}
\frac{1}{\sqrt{2} + \sqrt{5}} & = \frac{(\sqrt{2} – \sqrt{5})}{(\sqrt{2} + \sqrt{5})(\sqrt{2} – \sqrt{5})}\\
& = \frac{\sqrt{2} – \sqrt{5}}{2-5}\\
& = \frac{\sqrt{2} – \sqrt{5}}{-3}\\
& = \frac{(-1)(\sqrt{2} – \sqrt{5})}{(-1)(-3)}\\
& = \frac{\sqrt{5} – \sqrt{2}}{3}
\end{align}
となるよ。
近似値を求めるときはこれを利用すると計算が速いね!
上の式を$\sqrt{2} = 1.41421 \ \ , \ \ \sqrt{5} = 2.23606$ と考えて近似値を求めると
\begin{align}
\frac{1}{\sqrt{2} + \sqrt{5}} & = \frac{\sqrt{5} – \sqrt{2}}{3}\\
& \fallingdotseq \frac{2.23606 – 1.41421}{3}\\
& \fallingdotseq \frac{0.82185}{3}\\
& \fallingdotseq 0.27395
\end{align}
となるよ。
