平方根
2乗したら正の実数!

同じ数を2回掛けると、どんな実数も負にはならいない。
ちなみに、同じ数を2回かけることは2乗というよね。
2乗は、【正の数】×【正の数】 か 【負の数】×【負の数】のどちらかだから、何を2乗したのか聞かれたら、正の数(ココロの広いヤンキー点の実数)と負の数(ココロの狭いヤンキー点の実数)の2つを答える必要があるね。

なんだか、ついさっき実数の絶対値で見たのに似ている。

平方根って?
平方根の定義
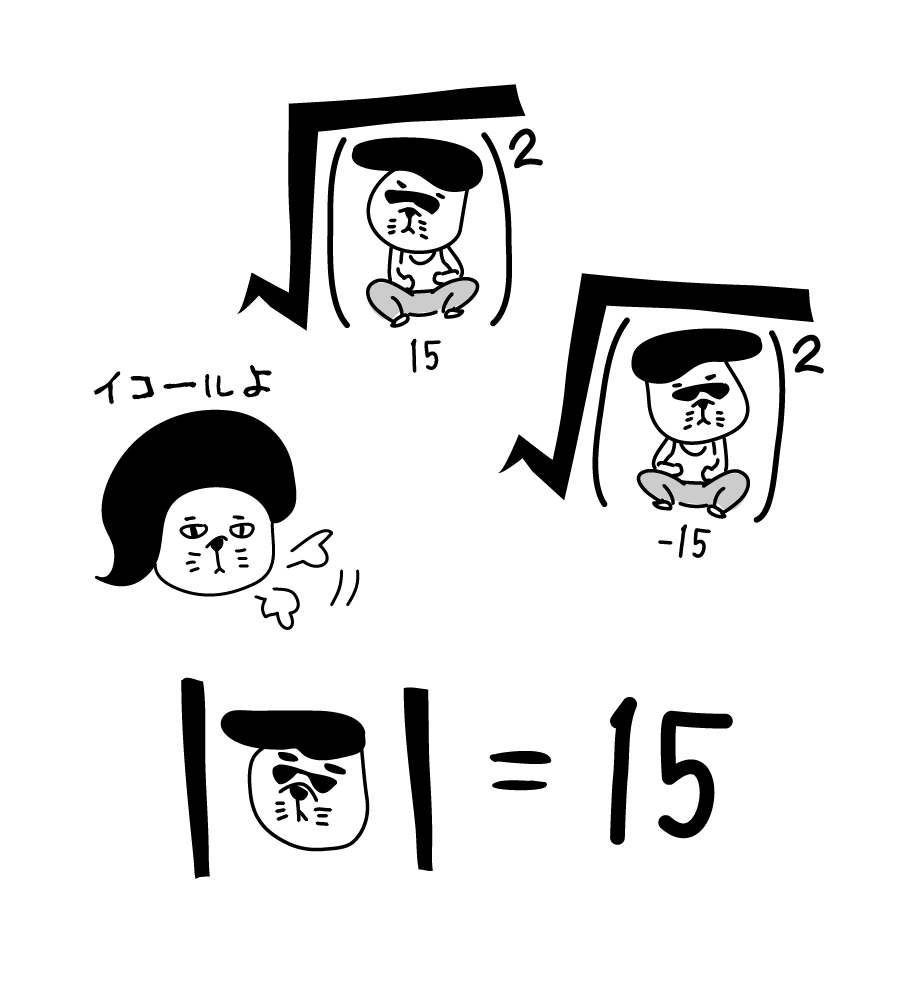
2乗してaになる数をaの平方根という。
aが正の実数のとき、aの平方根は実数の正と負の2つの数がある。正の平方根を$\sqrt{a}$で表し、負の平方根は$-\sqrt{a}$と書くことができる。
この記号$\sqrt{\ \ }$を根号という。
0の平方根は0だけのため、$\bf{\sqrt{0} = 0}$としよう。
平方根の定義から次のことがいえるよ。
- 平方根の性質
-
$[1] \ a \gt 0$ のとき $(\sqrt{a})^{2} = a$
\(
[2] \ \sqrt{a^{2}} = |a| =
\begin{cases}
a & ( a \ge 0 ) \\
-a & ( a \lt 0 )
\end{cases}
\)
※[1] $a<0$ の場合は $(\sqrt{a})^{2} = a$ にならないことに注意!!
平方根と数直線
$a$ を正の実数とすると $\sqrt{a}$ は数直線上でどこになるのか。
例えば $\sqrt{2}$ だとしたら
$\sqrt{2}$ は2乗して2になるのだから1よりは大きいけれど2よりは小さい。
$$1 \lt \sqrt{2} \lt 2$$
である。
なんとなく直感でわかるね。
では $\sqrt{50}$ はどうだろう??
こんなときは2乗して50より小さい平方数と50より大きい平方数を探してみよう。
50より小さい平方数は49,36,25,…で、50より大きい平方数は64,81,100,…だね。
直近の49と64を使って $49 \lt 50 \lt 64$ といえるね。

ということは $\sqrt{50}$ は $7$ よりは大きいけれど $8$ よりは小さいというのが分かるね。
数直線上ではどうやって点を落とせばよいかな?
こんなときは原点を中心に描く円と三平方の定理を活用するよ。
円の半径を $\sqrt{50}$ としよう。
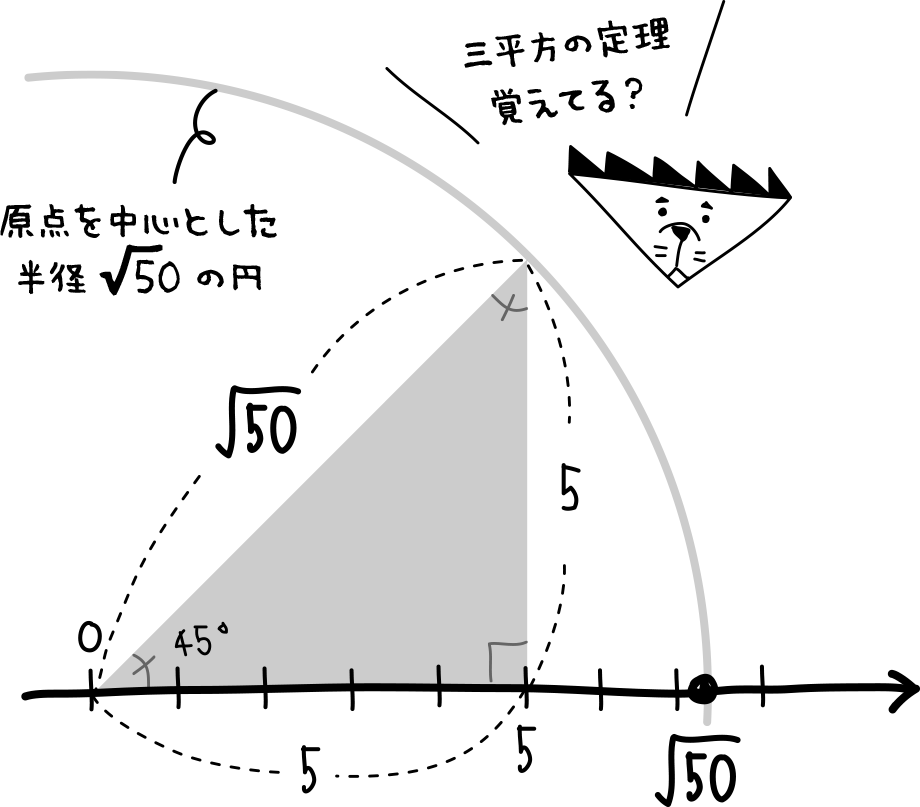
こうすれば $\sqrt{50}$ の点を数直線上に落とすことができるね。
- 三平方の定理(ピタゴラスの定理)
-
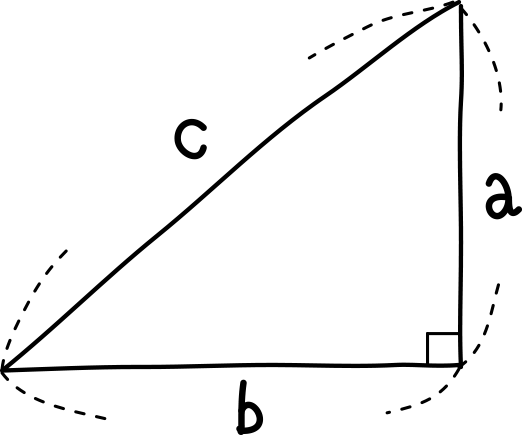
直角三角形の3辺の長さのうち、斜辺の長さをc、他の2辺の長さをa,bとするとき、
$$c^{2}=a^{2}+b^{2}$$
が成り立つ
