数学Ⅰ
実数の基本性質(3)
難易度.★
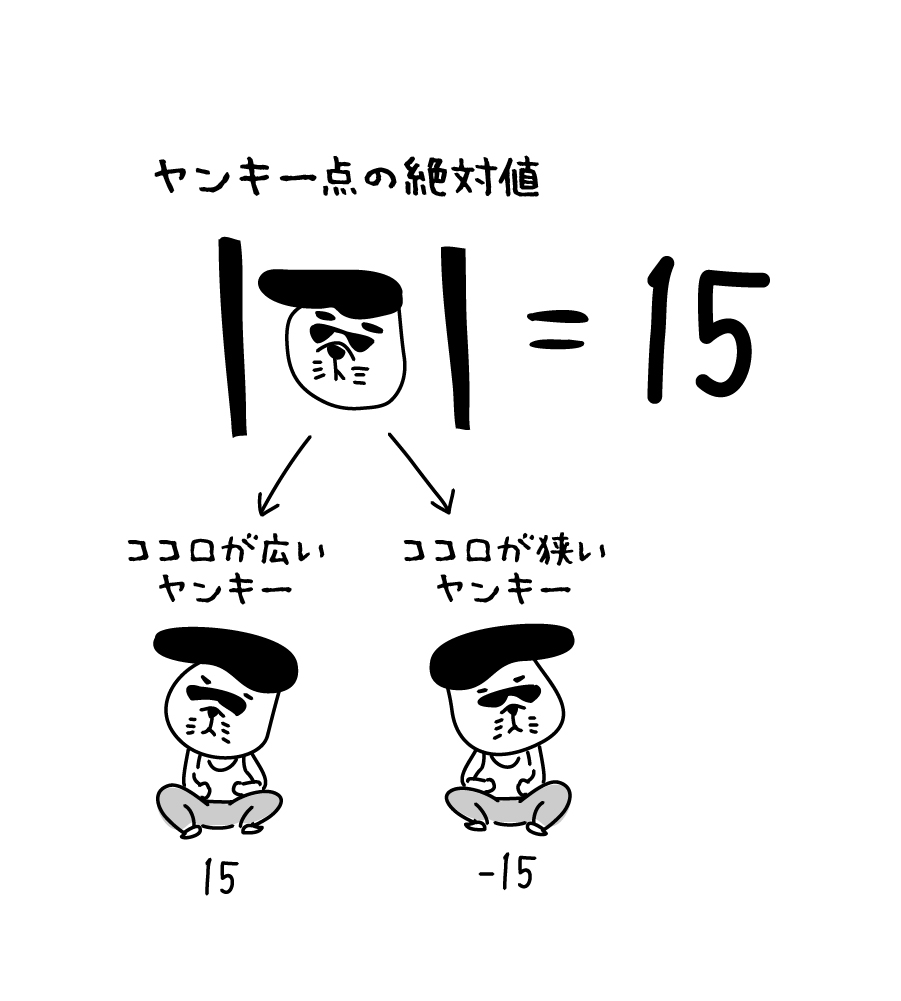
原点と点との距離を見つめて♥
直線に実数を対応させた数直線上の点同士の距離を見ていくよ。
まずは原点からの距離を見つめてみよう。
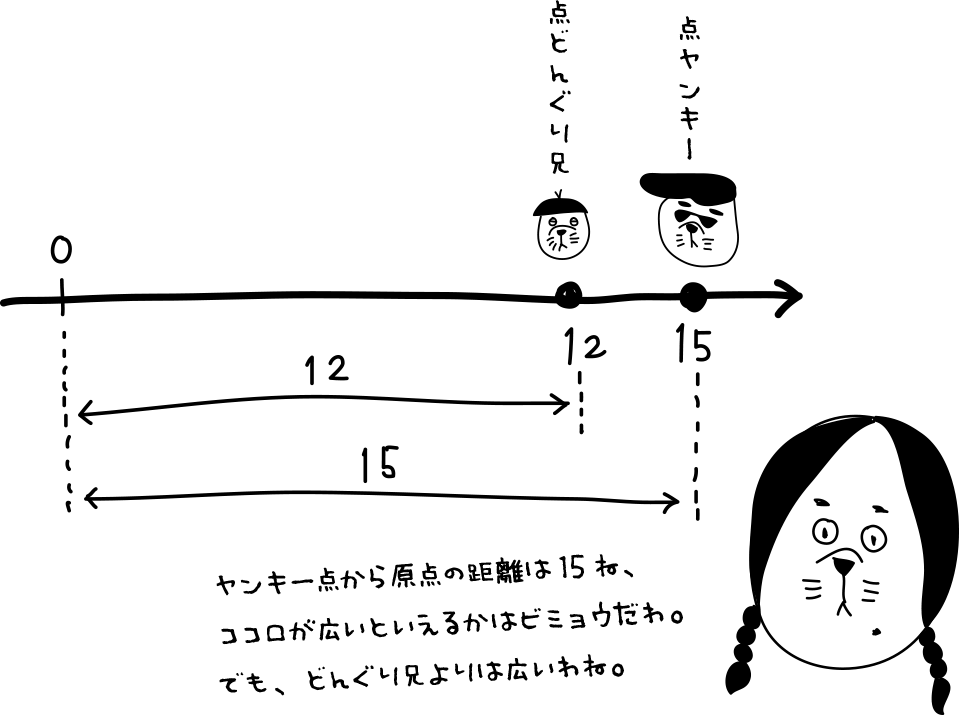
原点とヤンキー点との距離は15-0=15だね。
距離はどっちの点から見ても同じ距離だよね。

数直線の向きを考えると点の位置は、ヤンキー点から見たら原点は-15移動した場所だけど、原点から見たヤンキー点は15移動した場所・・・符号が変わってくる。
でも距離を考えるときは、向きを考える必要がないよね。だから距離が15の位置にある点は数直線上に2つ存在するのが分かるかい?!
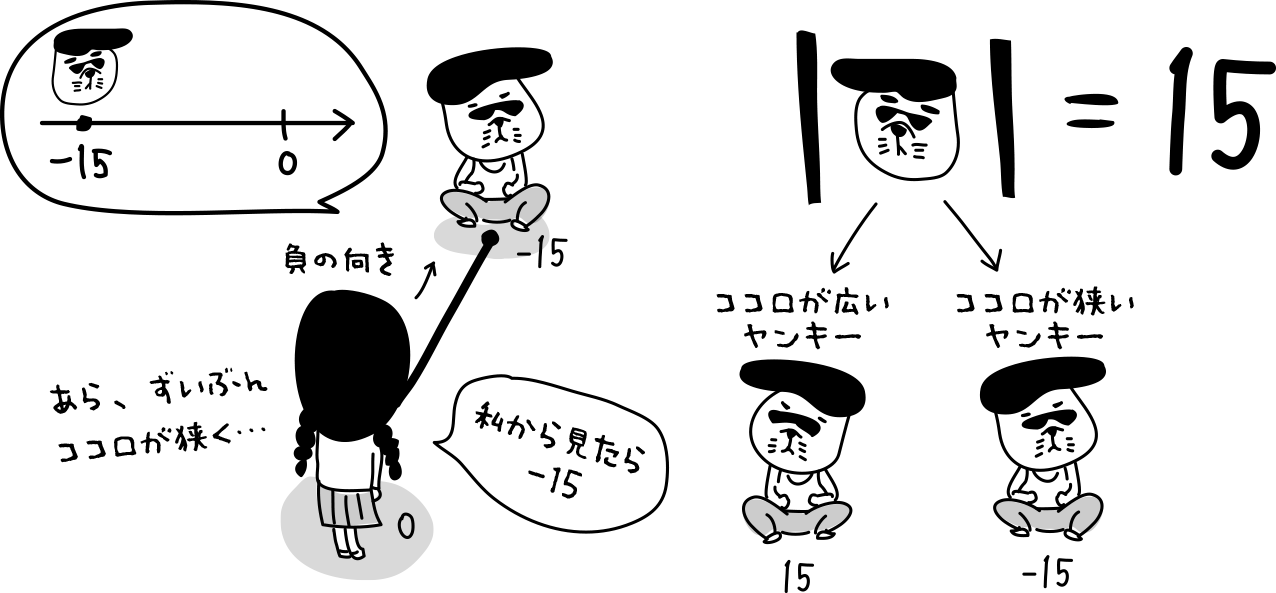
ココロの狭いヤンキー点も距離は15なんだよ!
実数の絶対値と数直線
実数の絶対値の定義
実数aに対して、垂直線上の点P(a)と原点Oとの距離をaの絶対値といって、|a|と表すよ。
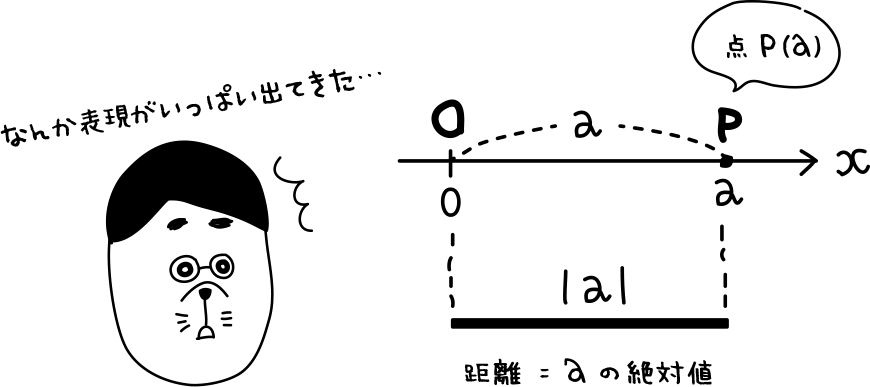
実数aをどんな実数xとして考えても、|x| = |-x|が成り立つ。
実数の絶対値の定義から次の性質が分かるよ。
- 実数の絶対値の性質
-
\[
|x|=
\begin{cases}
x & ( x \ge 0 ) \\
-x & ( x \lt 0 )
\end{cases}
\]
※xが負の数時は(-x)が正の数になるぞ!
数直線上の点同士の距離
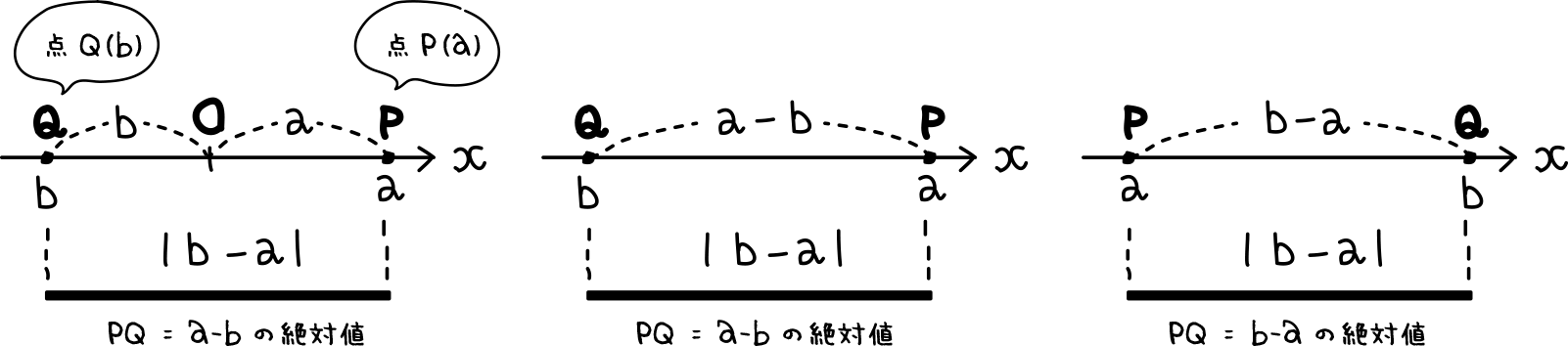
絶対値を利用して、数直線上の2つの点の距離を式で表すことができる。
上の図の点P(a)と点Q(b)の距離PQはPQ = |b-a|だね。
